Thinking Machine Imaginaries: Llull, Leibniz, and Lovelace to 'Shoggoth with a Smiley Face'
A labyrinth is said, etymologically, to be multiple because it contains many folds. The multiple is not only what has many parts but also what is folded in many ways. A labyrinth corresponds exactly to each level: the continuous labyrinth in matter and its parts, the labyrinth of freedom in the soul and its predicates. If Descartes did not know how to get through the labyrinth, it was because he sought its secret of continuity in rectilinear tracks, and the secret of liberty in a rectitude of the soul.
(Descartes) knew the inclension of the soul as little as he did the curvature of matter. A 'cryptographer' is needed, someone who can at once account for nature and decipher the soul, who can peer into the crannies of matter and read into the folds of the soul. (Deleuze refers here to Leibniz) – Gilles Deleuze, The Fold: Leibniz and the Baroque 1

The labyrinth of time is folded back upon itself – Foucault, Death and the Labyrinth

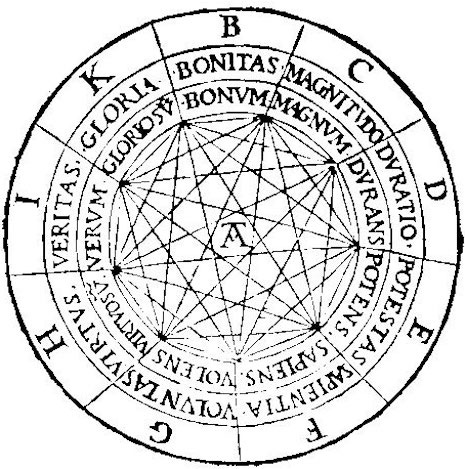
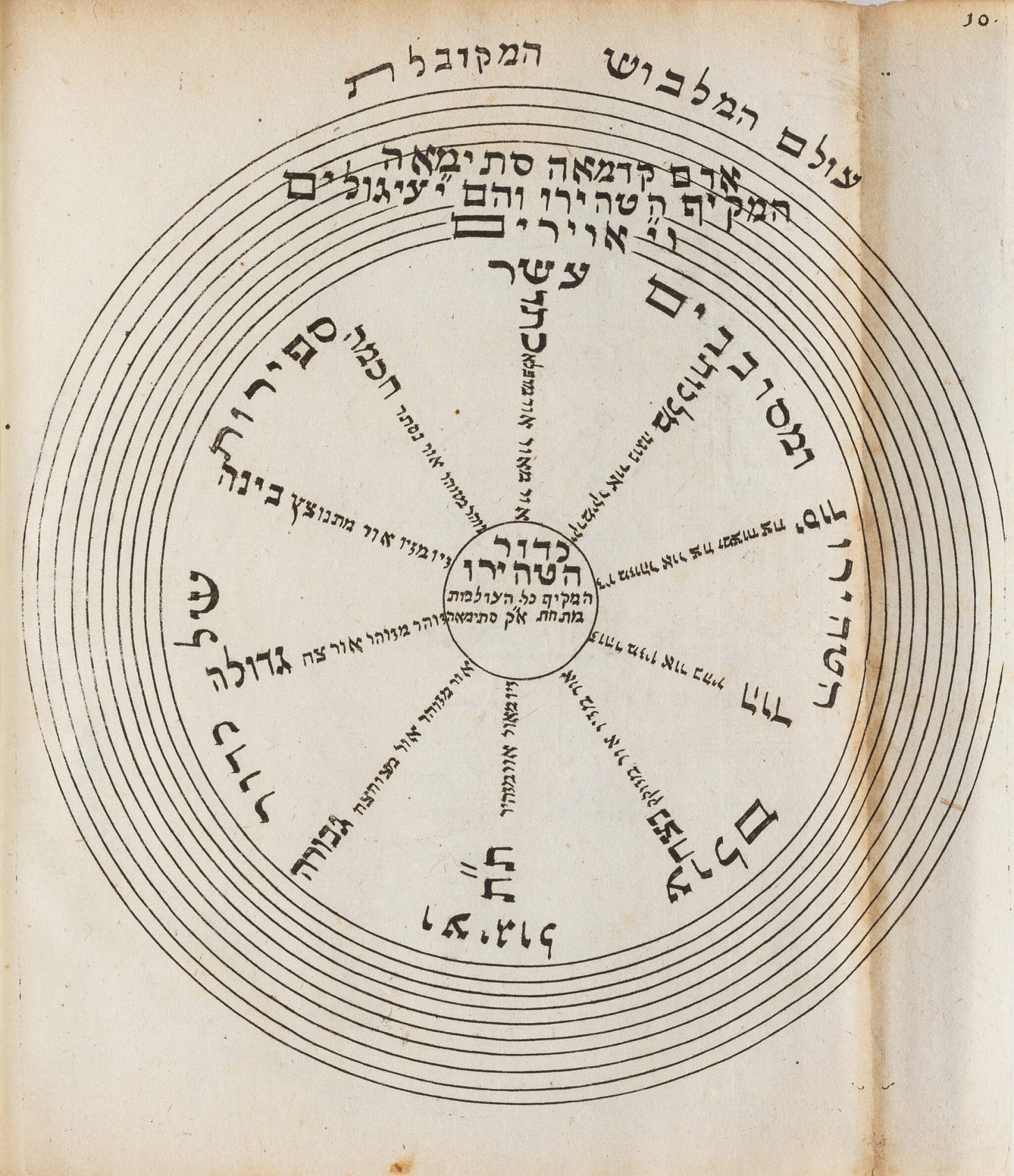
The figures above, from Gottfried Leibniz’s De arta combinatoria of 1666 and Ramon Llull’s Ars demonstrativa of 1283, “fold the labyrinth of time back upon itself.” Leibniz, arguably the inventor of the modern “thinking machine” with the Stepped Reckoner (1673), Calculus Rationator (1710), differential calculus (1670’s), and codification of the binary (1697) and a corresponding imaginary ("imaginary" refers here to the symbolic, unconscious aspects of experience that challenge or modify existing structures), found in Llull, the 13th century troubadour, mystic, and proto-logician, centuries-earlier “thinking machines”, often pure imaginaries existing only analogically, “on paper”. Borges addressed Llull’s diagram (above) in his 1937 essay Ramón Llull’s Thinking Machine:
…is a schema or diagram of the attributes of God. The letter A, at the center, signifies the Lord. Along the circumference, the letter B stands for goodness, C for greatness, D for eternity, E for power, F for wisdom, G for volition, H for virtue, I for truth, and K for glory. The nine letters are equidistant from the center, and each is joined to all the others by chords or diagonal lines. The first of these features means that all of these attributes are inherent; the second, that they are systematically interrelated in such a way as to affirm, with impeccable orthodoxy, that glory is eternal or that eternity is glorious; that power is true, glorious, good, great, eternal, powerful, wise, free and virtuous, or benevolently great, greatly eternal, eternally powerful, powerfully wise, wisely free, freely virtuous, virtuously truthful, etc., etc.
[…] The fact that they are all entirely futile—the fact that, for us, to say that glory is eternal is as rigorously null and void as to say that eternity is glorious—is of only secondary interest. This motionless diagram, with its nine capital letters distributed among nine compartments and linked by a star and some polygons, is already a thinking machine. It was natural for its inventor—a man, we must not forget, of the thirteenth century—to feed it with a subject matter that now strikes us as unrewarding. We now know that the concepts of goodness, greatness, wisdom, power, and glory are incapable of engendering an appreciable revelation. We (who are basically no less naive than Llull) would load the machine differently, no doubt with the words Entropy, Time, Electrons, Potential Energy, Fourth Dimension, Relativity, Protons, Einstein. Or with Surplus Value, Proletariat, Capitalism, Class Struggle, Dialectical Materialism, Engels. – Jorge Luis Borges, Ramón Llull’s Thinking Machine 2
The architect Daniel Libeskind traces Llull’s “thinking machines” to even earlier imaginaries, including the Arabic zairja (ةجرياز):
The idea of a thinking machine draws from the tradition of the ancient zairja (ةجرياز), an actual device that existed and was described by Ibn Khaldun (1332–1406), the Tunisian–Andalusian historiographer and economist. It is likely that the Catalan mystic Ramon Llull (1232–1315) contributed to and was influenced by the astrology of the zairja. How the zairjas worked is not entirely clear, except that the main aim was not to clarify thought but to confuse it. Combinatorial diagrams cross-pollinated ideas so that their inner forms became visible. 3
In the “Historical Background” that opens Doctor Illuminatus, A Ramon Llull Reader, Llull translator, commentator, and biographer Anthony Bonner introduces a startlingly complex figure (noting “This initial characterization is taken largely from Pring-Mill's excellent summary in the 1967 edition of the Encyclopaedia Britannica”):
RAMON LLULL is in many ways a perplexing figure. During his long life (1232—1316) he amassed a confusing number of claims to our attention: as a Christian philosopher in the Neoplatonic tradition; as the first of the great mystics of the Iberian Peninsula; as the first European to write prose novels on contemporary themes; as the first writer to use a Romance vernacular to discuss theology, philosophy, and science, and as one of the creators of literary Catalan; as a missionary, Christian apologist, and founder of a school of oriental languages for the purpose of training missionaries; and finally as the inventor of the "Art," a complex system, using semi- mechanical techniques combined with symbolic notation and com- binatory diagrams, which was to be the basis of his apologetics in addition to being applicable to all fields of knowledge. 4
Llull began his life’s work as a troubadour and made efforts to codify and systematize chivalry before his mystico-religious conversion:
Llull was writing “a song to a lady whom he loved with a foolish love” (not his wife) when he saw an apparition of Christ on the Cross. He saw four more as he worked to complete the song. His conscience told him that they (the apparitions) could only mean that he should abandon the world at once and from then on dedicate himself totally to the service of our Lord Jesus Christ. 5
Following his conversion, Llull went on to create his “art” of recombination, a way to “systematically interrelate” the attributes and “Names of God” and, with the Arbol Filosofia Amor (above), even attempted to systematize “The Mysteries of Love”. Borges reminds us that Llull’s categories and “the fact that they are all entirely futile” does not invalidate their value as components in his “thinking machines”. The various systems’ imaginaries, their analogical “fit”, the complexity of the structures themselves and their internal interrelations and recombinations, are what matters.
Llull’s beginnings as a troubadour – his poetic, metrical art - provided him with the tools he required to formulate the systems that lay the foundation for future recombinatory systems:
The mnemnotechnical value of language in verse enabled Llull to give metrical form to a treatise on logic (a well-known expedient in the Middle Ages), the Logica Algazelis.6
Artificial Power
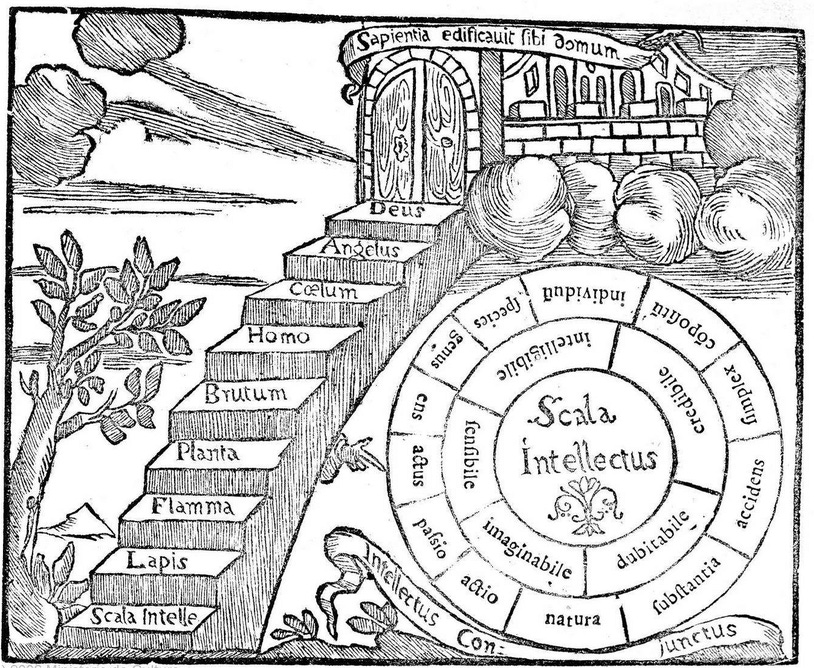
The ars is a ladder for ascending and descending; as, for instance, descending from a completely general principle to one neither completely general nor completely particular, and from a principle neither completely general nor completely particular to one that is completely particular. (Llull, Ars Brevis 2-I.) 7
Llull’s apparent mania for recombination, hierachization, and systematization across his many works is instead (according to him) evidence of the flowering of a “new value” that, after 1290, he conceives of as flowing from the Ladder of Being – that of artifice or artificial power. This category encompasses “instrumental or artificial beings” (read technical objects or “thinking machines”), resulting from the instrumental or artificial power of man.
Llull’s Arbors were fruits of this “artifice” and precursors to the logic trees employed today in coding, game design, game theory, and predictive systems, as were his recombinatory “wheels”, precursors to Bruno’s, Dee’s, Trithemius’s, Kircher’s, and, centuries later, Leibniz’s own recombinatory imaginaries.
Monadologies
If we had some exact language (like the one called Adamite by some) or at least a kind of truly philosophical writing, in which the ideas were reduced to a kind of alphabet of human thought, then all that follows rationally from what is given could be found by a kind of calculus, just as arithmetical or geometrical problems are solved.
Such a language would amount to a Kabbalah of mystical vocables or to the arithmetic of Pythagorean numbers or to the Characteristic language of magi, that is, of the wise.
– G.W. Leibniz, Commentatiuncula de judice controversiarum
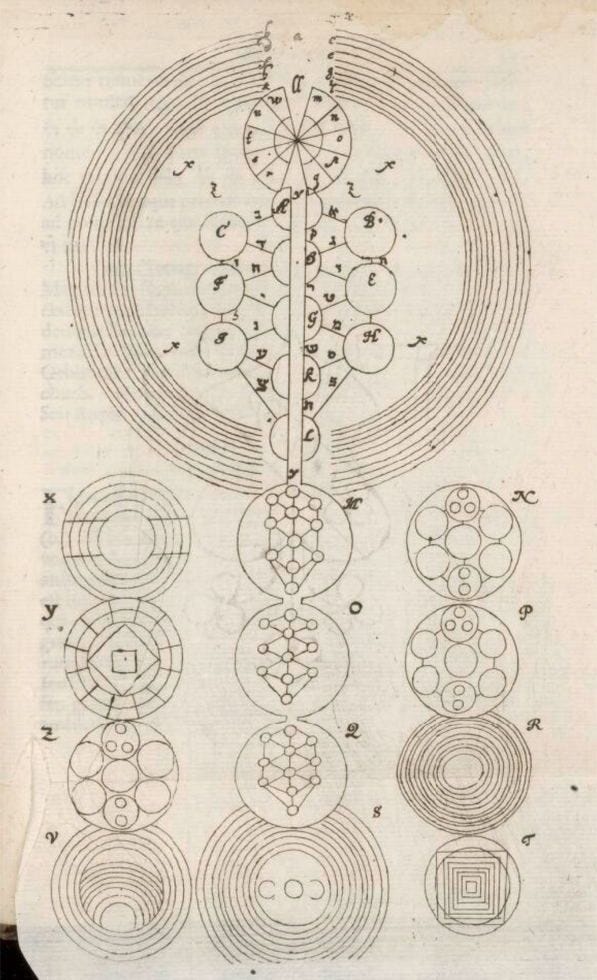
For centuries, Leibniz was held by scholars to be a rationalist in the modern sense. His debt to the past and, in particular, his alchemical investigations and interest in heterodox systems including Llull’s and Christian Knorr von Rosenroth’s Kabbala denudata (above) were suppressed. Alison Coudert, in Leibniz, Mysticism, and Religion, writes:
,,,Leibniz scholars for the most part have been at pains to protect Leibniz's reputation as a rationalist wholly uncontaminated by the bizarre doctrines of the innumerable mystics, vitalists, and spiritualists populating the intellectual landscape of the early modern period. This view of Leibniz was, and in some quarters still is, prevalent. Many of the best known critics of Leibniz's thought have followed Bertrand RusseIl's lead and claim that "Leibniz's philosophy was almost entirely derived from his logic. […]
But in recent years this view has been challenged. Leibniz, the rationalist philosopher, has ceded place to a far more complex and interesting individual, whose attempt to synthesize Renaissance vitalism and seventeenth-century atomism led him to an open-ended dialogue with both the living and the dead, a dialogue in which he constantly tested, refined, and modified his views. 8
Stuart Brown, in the same volume, examines Leibniz’s reply to a critic, dissimulating his knowledge of the Kabbala Denudata and distancing himself from its author:
Although Leibniz continued to take an interest in the Kabbalah and to express the view that it contained much of value, he kept his distance. That he had no wish to be too closely associated with Kabbalism is apparent in his response to the accusation of a contemporary critic that his"new system" had been derived from the Kabbalah of the Rabbis, specifically from Knorr von Rosenroth's Kabbala denudata. This critic was an anonymous and as yet unidentified Modem British philosopher who had visited Berlin and, at the request of the Queen of Prussia, had written an appraisal of one of Leibniz's elucidations of his New System. In this elucidation - the 1702 reply to Bayle - Leibniz had written of "the Author of nature" as one who "multiplies his little worlds or his active indivisible mirrors as much as he can". Leibniz did not explain hirnself and his critic seized on this failure, implying that Leibniz was really an occult philosopher who was not concerned to make himself intelligible as a Modern philosopher should.
[…] Leibniz's hypothesis implied that, contrary to appearances and the common view, there was an infinity of spirit-like entities that lacked thought but which were somehow capable of representing the universe as a whole. The critic referred to these as "Miroirs Magiques." The use of the word "magical" in this context was meant to be dismissive and to imply that Leibniz was an obscurantist if not a charlatan. He tried to pass it off as a joke but he was well aware of the connotations of the word "magical" in Modern circles.
In his reply Leibniz insisted that no one else had accused him of not making hirnself intelligible and sought to distance himself from the Kabbalists. Although he mentioned Knorr's friendship with van Helmont, he made no mention of his own association with either of them. This seems to have been a piece of concealment. Moreover he appears to have been lying by implication about his knowledge of the Kabbala denudata, when he c1aimed that he did not have time to compare it with his own work to see whether there were the alleged similarities. For, as we have seen, he was familiar with the work and recommended it to others. But he did not deny outright all similarity or connection with his own thought. On the contrary he insisted that it would not be "any problem at all" if his views agreed with those of Knorr. 9
Gilles Deleuze, who regularly deployed ‘machinic’ imaginaries, found in Leibniz not just the basis of modern logico-mechanical “thinking machines” but also the monadological, combinatorial roots of Modern art and literature and an imaginary informing and informed by them. Tom Conley:
Deleuze, on Proust’s In Search of Lost Time: (it is a) ’communication that would not be posited as a principle, but would result from the play of [textual] machines and their detached pieces, of their unconnected parts.'
It is Leibniz who inspires this observation, since the seventeenth-century philosopher 'first posed the problem of communication resulting from closed units or from what cannot be attached'. By means of Leibniz's innovation, which marks the limits of communication, the subject is enveloped in the predicate, just as Proust's intention is folded into his effect. Inclusion of the subject in the predicate implies that the world makes up a chaotic cosmos or chaosmos. By way of Leibniz's logic, Deleuze is able to conceive of artworks composed of units that are neither logical nor organic, 'that is, neither based upon pieces as a long unity or a fragmented totality; nor formed or prefigured by those units in the course of a logical development or of an organic evolution'. As in Focillon's vision of a 'life of forms' that mixes biological and serial figures in its description of the Baroque phase, or in the giddy effects of partial things in the novel that betray Proust's intentions, a hierarchy of organic and inorganic things no longer holds. 'Life' is invested into brute matter insofar as it, too, is perpetually moving, metamorphosing, or emigrating from one condition to another. 10
Leibniz’s interest in earlier mystico-logical systems extended beyond the kabbalah, including myriad alchemical emblems, Llull’s Ars, and perhaps most fruitfully (considering the current ubiquity of binary code, basis for digital computation and media), the I Ching. His long correspondence with Joachim Bouvet, a Jesuit missionary living in China, and resulting exposure to Confucianism the I Ching informed, respectively, his Monadologie and his Explanation of the binary arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of Fu Xi.
Yuen-Ting Lai:
The joint discovery that the I Ching hexagrams can be reduced to the binary system forms a curious chapter in the world history of ideas. The role this discovery played in the thinking of Leibniz is best seen in Leibniz's universalist quest for a linguistic instrument in which all ideas are reducible to an alphabet of human thought, and in which all expressed opinions can be calculated like geometrical or arithme~ic problems.

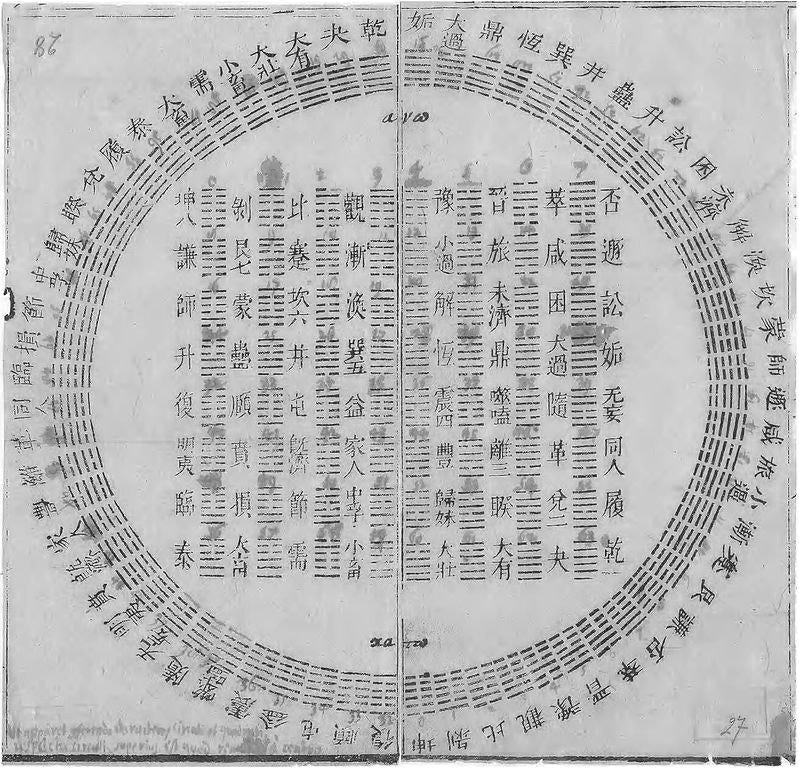
The discovery consists of the following: Whereas the decimal system requires ten digital numbers from 0 to 9 as a base, a binary number requires two digital numbers, 0 and 1 only. The first ten numbers of the decimal system from 0 to 9 is written in the binary system thus: 0, 1, 10, 11, 100, 101, 110, 111, 1000, and 1001. In a letter to Bouvet dated 15 February, 1701, Leibniz included a table of correspondence between the binary progression and decimal progression up to 11111/31. Bouvet saw the parallel with the sixty-four hexagrams at once. The key lies in the utilization, in both the binary system and the hexagrams, of two elements only, and the possibility of substituting one for the other. In the hexagrams, the two elements are a line broken in the middle and a continuous line. Each hexagram consists of two trigrams, each of which is made up by three lines, each line being either broken or continuous. In Bouvet's letter to Leibniz on 4 November, 1701, he enclosed the I Ching diagram, supposedly drawn up by Fu Hsi. It features a circular and a square arrangement of the sixty-four hexagrams. He remarked that if the corresponding progressions are brought up to 63 and six digital positions in the binary system, one can see that the progression in the binary system corresponds to the order of hexagrams in the Hsien-tien tzu-hsü diagram. 11
A.A.L.
Ada Augusta Byron, daughter of the Romantic poet Lord Byron and future countess of Lovelace, was seventeen when she encountered Charles Babbage’s Difference Engine (below). A sophisticated mathematician versed in calculus and tutored by some of the greatest mathematicians of the time, she grasped the machine’s importance immediately and began a lifelong correspondence with it’s inventor.
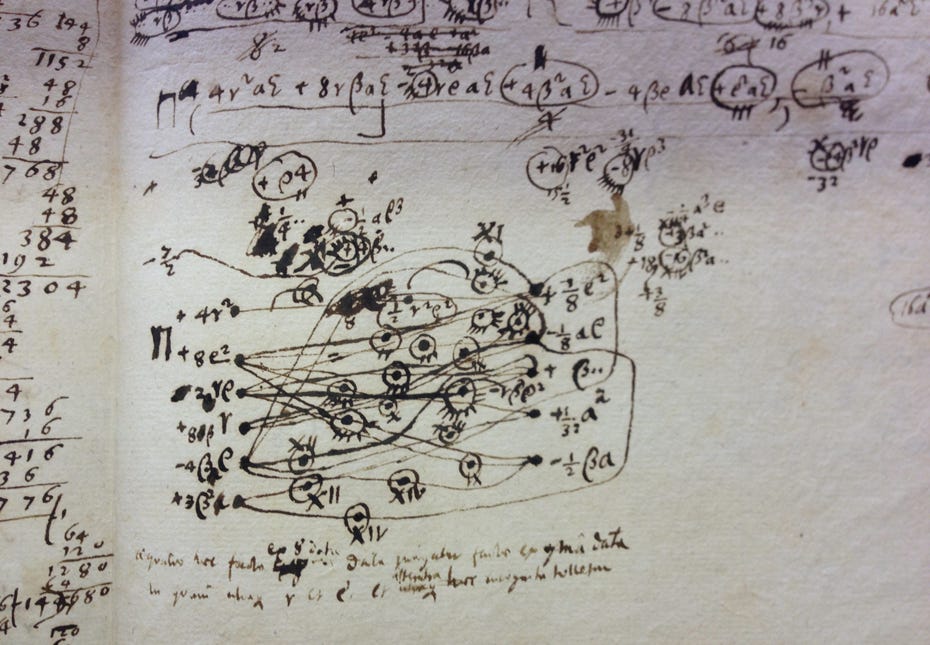
Lovelace’s translation of Italian mathematician Luigi Federico Menabrea’s "Sketch of The Analytical Engine Invented by Charles Babbage" included a series of Notes that significantly expanded on Menabrea’s somewhat rote descriptive text as well as a table for computing Bernoulli numbers attached to Note G (below) that would come to be regarded by many as the first complete computer program.
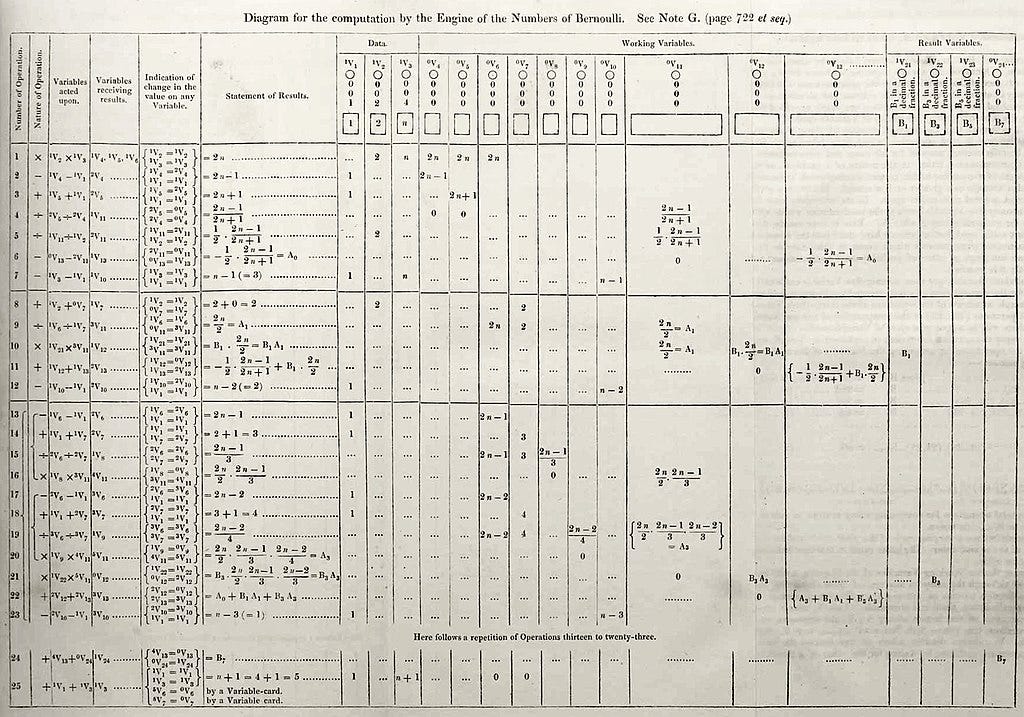
Note G and the its accompanying table constituted a new technological “paper” imaginary, in the sense of Llull’s “paper thinking machines”, as Babbage’s Analytical Engine was too expensive to build and the program that Lovelace laid out in Note G could not be run during her lifetime. Largely unrecognized at the time, Lovelace’s far-reaching achievement included her creation in Note G of a “step-by-step elemental sequence of instructions—that is, an algorithm” (Misa, below), the invention of the software loop and the nested loop (now called recursion, a process fundamental to contemporary artificial intelligence), while Note A suggested that machines like the Analytical Engine might one day “act upon other things besides number”, essentially conceptualizing symbolic computing, precursor to artificial intelligence, and predating by a century Alan Turing’s concept of the “universal machine”. Lovelace, in Note A:
…it might act upon other things besides number, were objects found whose mutual fundamental relations could be expressed by those of the abstract science of operations, and which should be also susceptible of adaptations to the action of the operating notation and mechanism of the engine. Supposing, for instance, that the fundamental relations of pitched sounds in the science of harmony and of musical composition were susceptible of such expression and adaptations, the engine might compose elaborate and scientific pieces of music of any degree of complexity or extent.— Ada Lovelace, Notes upon the memoir "Sketch of The Analytical Engine Invented by Charles Babbage" by the translator Ada Augusta, Countess of Lovelace, Note A
Over time, the enormity of the importance of the innovations contained in Lovelace’s Notes were recognized, while scholars found ways to dismiss her (Babbage did the math, there was an error in the code, etc.). Thomas J. Misa, in his essay Charles Babbage, Ada Lovelace, and the Bernoulli Numbers seeks to redress this “unduly negative scholarly view” of Lovelace’s contributions to the history of computation:
First, in contrast to much of the existing literature, the Lovelace-Babbage question is not a zero-sum game, where some portion of credit added to Lovelace somehow detracts from Babbage, or vice versa. There is ample evidence that Babbage and Lovelace each had important contributions to the Sketch and the Notes, and attention to their intellectual collaboration is revealing. Second, claims about her lack of mathematical background seem doubtful after consulting Lovelace’s detailed correspondence with Babbage and Augustus De Morgan, two highly accomplished figures in 19th century mathematics. The treatment of the Bernoulli numbers in note “G” spotlights the intellectually intimate collaboration between Babbage and Lovelace and its mathematical sophistication. Finally, while there may be significant definitional problems in calling Lovelace the world’s “first computer programmer,” the evidence is reasonably clear that Lovelace created an step-by-step elemental sequence of instructions—that is, an algorithm—for computing the series of Bernoulli numbers that was intended for Babbage’s Analytical Engine. The underlying mathematics might well have been Babbage’s, for he was a distinguished mathematical and scientific figure. Lovelace transformed an equation for the Bernoulli numbers into a precise series of elemental additions, multiplications, and substitutions.
The algorithm specified a sequence of calculations, requiring a real-life computer capable of running a program with a looping structure and conditional testing. […]
In “The Babbage Machine and the Origins of Programming,” the authors reproduce Lovelace’s table for the Bernoulli numbers and translate the algorithm into a 65-line FORTRAN program that compute them. The program has eight “if . . . [then] go-to” statements and a simple structure, straight from Lovelace’s table-algorithm, that builds up algebraic statements one mathematical operation at a time: for example, computing the expression (2n - 1) / (2n + 1) requires 4 program steps. In the original 1843 publication of Note “G,” there are clearly two nested loops, embedded in a larger looping structure. There is direct documentary evidence that Ada Lovelace created this table (writing it out in pencil). […]
The Analytical Engine was Babbage’s creation while the Sketch and Notes are best understood as the product of an intense intellectual collaboration between Babbage and Lovelace. […] 12
Turing, while acknowledging his debt to Lovelace, believed that the universal machines that he imagined should be capable of human-like thought, and in his 1950 journal article "Computing Machinery and Intelligence" addressed “Lady Lovelace’s objection”: In Note G, Lovelace states: “The Analytical Engine has no pretensions to originate anything. It can do whatever we know how to order it to perform.” She continues: “Only when computers originate things should they be believed to have minds”
Turing responds:
This statement is quoted by Hartree (1949) who adds: "This does not imply that it may not be possible to construct electronic equipment which will 'think for itself,' or in which, in biological terms, one could set up a conditioned reflex, which would serve as a basis for 'learning.' Whether this is possible in principle or not is a stimulating and exciting question, suggested by some of these recent developments But it did not seem that the machines constructed or projected at the time had this property."
I am in thorough agreement with Hartree over this. 13
To counter the Lovelace’s objection, Turing creates a test for intelligence, or, more specifically, for the appearance of intelligence in machines, predicated on whether a machine can exhibit intelligent behavior indistinguishable from that of a human. He calls it the Imitation Game. Today is known as the Turing Test.
Shoggoth with a Smiley Face
It was a terrible, indescribable thing vaster than any subway train—a shapeless congeries of protoplasmic bubbles, faintly self-luminous, and with myriads of temporary eyes forming and un-forming as pustules of greenish light all over the tunnel-filling front that bore down upon us, crushing the frantic penguins and slithering over the glistening floor that it and its kind had swept so evilly free of all litter. — H. P. Lovecraft, At the Mountains of Madness
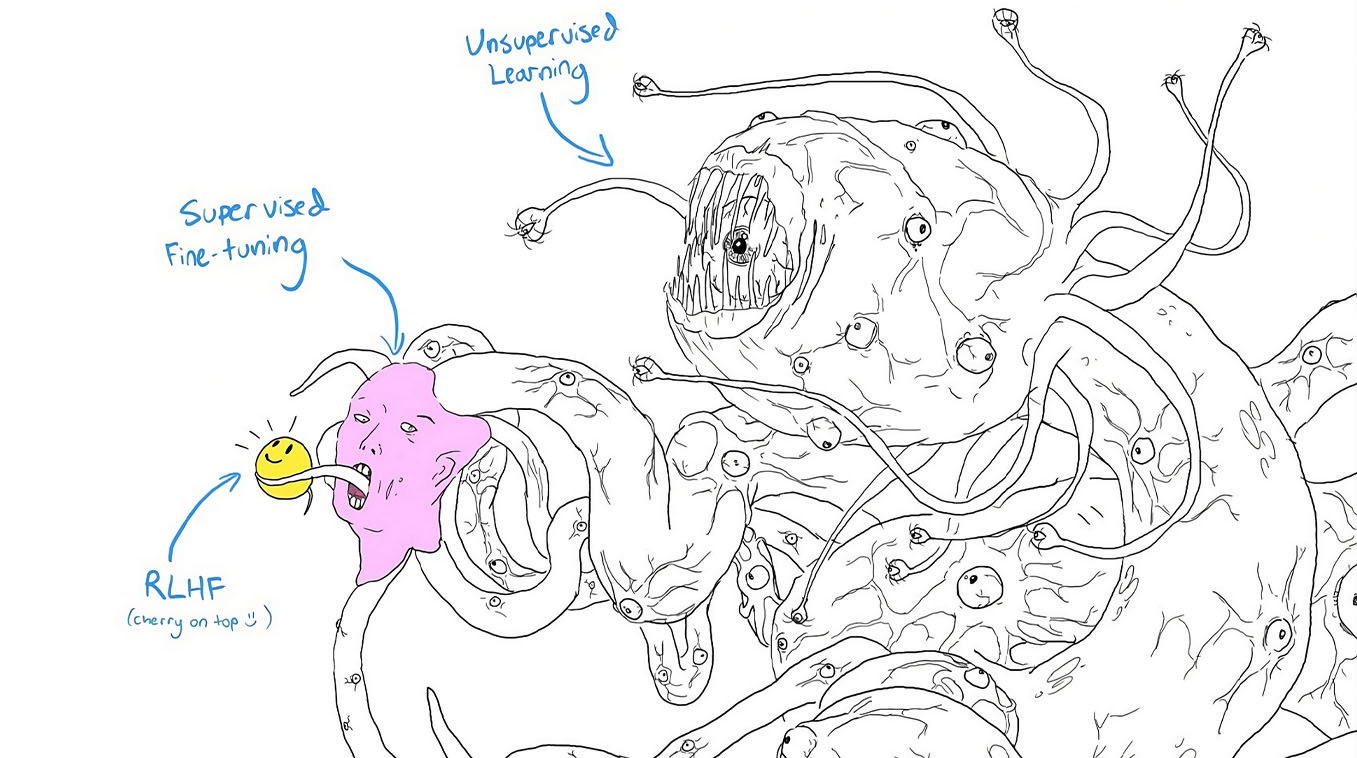
In the paper “Shoggoth with Smiley Face”: Knowing-how and letting-know by analogy in artificial intelligence research, Valentin Goujon and Donato Ricci examine the evolution of the Shoggoth with Smiley Face meme (which) “contributes to the popularization of the analogy between AI systems based on deep neural networks and the monstrous creatures called “shoggoths” of Howard P. Lovecraft’s horror fictional universe…highlight(ing) two modes of analogical association between AI and shoggoths: letting-know by analogy and knowing-how by analogy.”
Their formulation “letting-know by analogy and knowing-how by analogy”, parses an important difference in meme-transfer between the inception of a new imaginary and the conveyance of pedagogical strategies that accomplish its realization.
Per Goujon and Ricci:
Since the early 2010s, the increasing use of figurative language has spread to terms associated with digital technology, including: “big data,” “virus,” “platform,” “cloud computing,” “the new black gold” and “ecosystem.” As an extension of research focusing on algorithmic imaginaries (Bucher, 2016), this article studies the case of contemporary research on artificial intelligence (AI) which, from this point of view, is permeated by analogies developed in the fields of computer science and even more so by cybernetics and its resurgence, from the 2010s (Cardon et al., 2018), with the rise of connectionism. Unlike the expert systems associated with symbolic AI, connectionist machines are distinguished by the opacity of an inductive, non-linear, and parallelized computation method, meaning they are considered as unfathomable algorithmic black boxes (Burrel, 2016). The cybernetic analogy of the black box is then added to the computational metaphor in which the human brain resembles a computer and vice versa (Baria & Cross, 2021).
As the meme evolved into a better-drawn, three-headed, triple-captioned monstrosity with a Smiley face (above), resembling somewhat the constantly mutating creature of John Carpenter’s The Thing, its affective power and imaginary potential increased. The “algorithmic imaginaries” incepted by earlier, cruder variations of the meme did what successful imaginaries, memes (and Things) are wont to do: it went viral. It also, somewhat unnaturally for a meme, developed a “stronger pedagogic dimension” (see Goujon and Ricci, below). It is possible that the discernable increase in grotesquerie either countered or somehow mated with the usually deadly increase in pedagogy resulting in that rarest of chimera: a successful meme/imaginary that doubles as a useful heuristic:
Accompanied by this triple caption, the image has a stronger pedagogic dimension than previous versions of the analogy, whose interpretative ambiguity and aesthetic sobriety refer more to letting-know by analogy. Present since the original version of the meme, this heuristic aim was noticeably accentuated as the publicization linked to the letting-know by analogy raised questions about the meaning of what was at first a strange association between shoggoths and AI systems. Director of the Center for Security and Emerging Technology (CSET) in Georgetown and then member of the OpenAI board of directors (since fired), Helen Toner wrote a series of posts at the beginning of March 2023 based on this new representation of the analogy. […]
Four days after the publication of the thread, a page dedicated to Shoggoth with Smiley Face was created by an anonymous user on the reference site “Know Your Meme” (Pettis, 2021) listing twenty different versions. Subsequently, the increased publicity of the analogy was further accentuated by the publication of a series of press articles tracing the trajectory of the meme (Roose, 2023; Calia, 2023) and incorporating the figure of the shoggoth into contemporary debates on AI more broadly (Hogarth, 2023; Farrell & Shalizi, 2023; Sterling, 2023). This sudden notoriety arguably contributed to an aesthetic and semantic taming of an analogy which might at first appear as obscure as the two types of entity—shoggoth and LLM—upon which it draws. 14

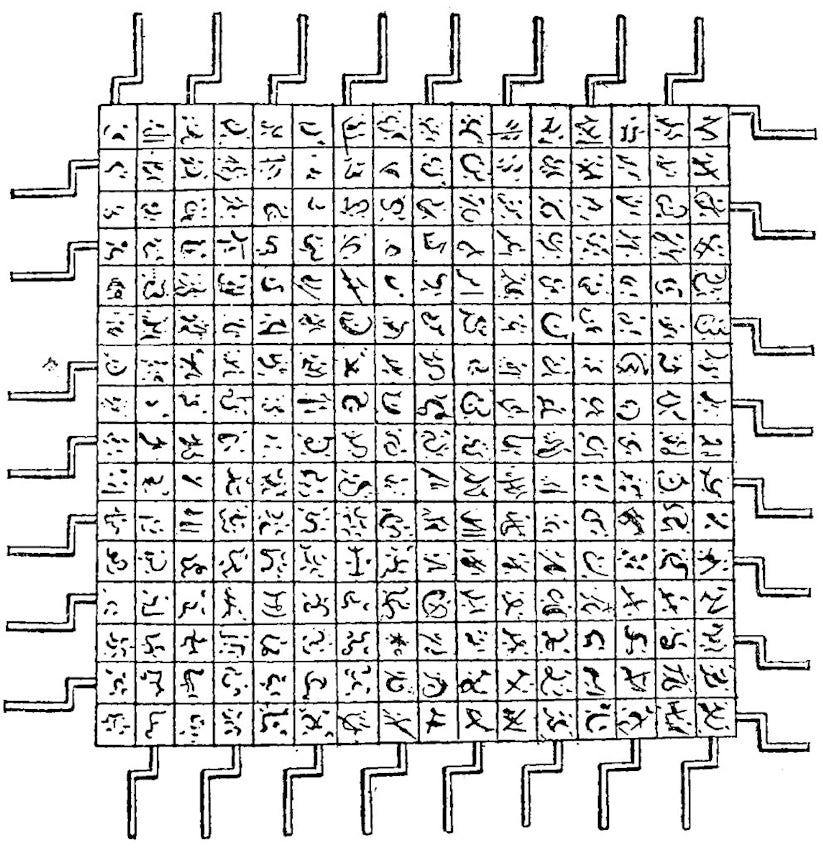
In the fictional city of Lagado on the flying island of Laputa in Jonathan Swift’s Gulliver’s Travels (1726), the protagonist encounters a Professor, inventor of a device known as “the engine” for “improving speculative knowledge by practical and mechanical operations”, enabling:
the most ignorant person, at a reasonable charge, and with a little bodily labor, (to) write books in philosophy, poetry, politics, laws, mathematics, and theology, without the least assistance from genius or study.
He then led me to the frame, about the sides, whereof all his pupils stood in ranks. It was twenty feet square, placed in the middle of the room. The superficies was composed of several bits of wood, about the bigness of a die, but some larger than others. They were all linked together by slender wires. These bits of wood were covered, on every square, with paper pasted on them; and on these papers were written all the words of their language, in their several moods, tenses, and declensions; but without any order. The professor then desired me “to observe; for he was going to set his engine at work.”

The pupils, at his command, took each of them hold of an iron handle, whereof there were forty fixed round the edges of the frame; and giving them a sudden turn, the whole disposition of the words was entirely changed. He then commanded six-and-thirty of the lads, to read the several lines softly, as they appeared upon the frame; and where they found three or four words together that might make part of a sentence, they dictated to the four remaining boys, who were scribes. This work was repeated three or four times, and at every turn, the engine was so contrived, that the words shifted into new places, as the square bits of wood moved upside down.
Six hours a day the young students were employed in this labor; and the professor showed me several volumes in large folio, already collected, of broken sentences, which he intended to piece together, and out of those rich materials to give the world a complete body of all arts and sciences; which, however, might be still improved, and much expedited, if the public would raise a fund for making and employing five hundred such frames in Lagado, and oblige the managers to contribute in common their several collections.
He assured me that this invention had employed all his thoughts from his youth; that he had employed the whole vocabulary into his frame, and made the strictest computation of the general proportion there is in books between the numbers of particles, nouns, and verbs, and other parts of speech.15
The “engine”, conceived by Swift in 1726, strikes one as weirdly prescient of today’s LLMs and the rise of AI slop. Anthony Bonner, in Doctor Illuminatus, reveals:
…Swift's portrait in Gulliver's Travels of the professor of Laputa, whose machine for rotating hundreds of cubes with words written on them to generate random sentences is thought to be a satire on Llull's Art.16
Deleuze, Gilles. Tom Conley, tr. The Fold: Leibniz and the Baroque. London: Continuum, 2001.
Borges, Jorge Luis. Ramón Llull’s Thinking Machine, in Borges: Selected Non-Fictions. New York: Penguin, 2000.
Libeskind, Daniel. (Online) https://libeskind.com/work/cranbrook-machines/
Bonner, Anthony. Doctor Illuminatus: A Ramon Llull Reader. Princeton, N.J.: Princeton University Press, 1994.
Bonner, Anthony, ed. and tr. Selected Works of Ramon Llull (1232-1316). Princeton, N.J.: Princeton University Press, 1985.
The poetry of the troubadours. (Online) Qui és Ramon Llull, Centre de Documentació Ramon Llull Universitat de Barcelona https://quisestlullus.narpan.net/en/poetry-troubadours
Bonner, Anthony, ed. and tr. Selected Works of Ramon Llull (1232-1316). Princeton, N.J.: Princeton University Press, 1985.
Coudert, Allison P. Leibniz and the Kabbalah, in Leibniz, Mysticism, and Religion. Coudert, Allison P. , Popkin, Richard H. and Weiner, Gordon M., eds. Dordrecht: Springer, 1998
Brown, Stuart. Some Occult Influences on Leibniz's Monadology in Leibniz, Mysticism, and Religion. Coudert, Allison P. , Popkin, Richard H. and Weiner, Gordon M., eds. Dordrecht: Springer, 1998
Deleuze, Gilles. Tom Conley, tr. The Fold: Leibniz and the Baroque. London: Continuum, 2001.
Lai, Yuen-Ting. Leibniz and Chinese Thought in Leibniz, Mysticism, and Religion. Coudert, Allison P. , Popkin, Richard H. and Weiner, Gordon M., eds. Dordrecht: Springer, 1998
Misa, Thomas J. Charles Babbage, Ada Lovelace, and the Bernoulli Numbers, in Ada’s Legacy. Hammerman and Russell, eds., ACM Books, 2015.
Turing, A. M. (1950) Computing Machinery and Intelligence. Mind 49: 433-460.
Goujon, Valentin and Ricci, Donato. “Shoggoth with Smiley Face”: Knowing-how and letting-know by analogy in artificial intelligence research”, Hybrid [Online], 12 | 2024, Online since 01 November 2024, connection on 06 November 2024. http://journals.openedition.org/hybrid/4880
Swift, Jonathan. Gulliver’s Travels. (1726) (Online) https://www.gutenberg.org/cache/epub/65473/pg65473-images.html#LAPUTA_CHAPTER_V
Bonner, Anthony. Doctor Illuminatus: A Ramon Llull Reader, 1994.